Decision Trees: Eliminating Uncertainty in the Decision-Making Process
Every day, designers are faced with decision-making challenges on different levels of their careers. In many of these situations, uncertainty dominates the choices, especially when it comes to evaluating new ideas or innovating new products. Decision trees are considered an efficient method to make decisions or solve problems under uncertainty in order to evaluate each choice based on the outcome and compare choices based on these expected outcomes.
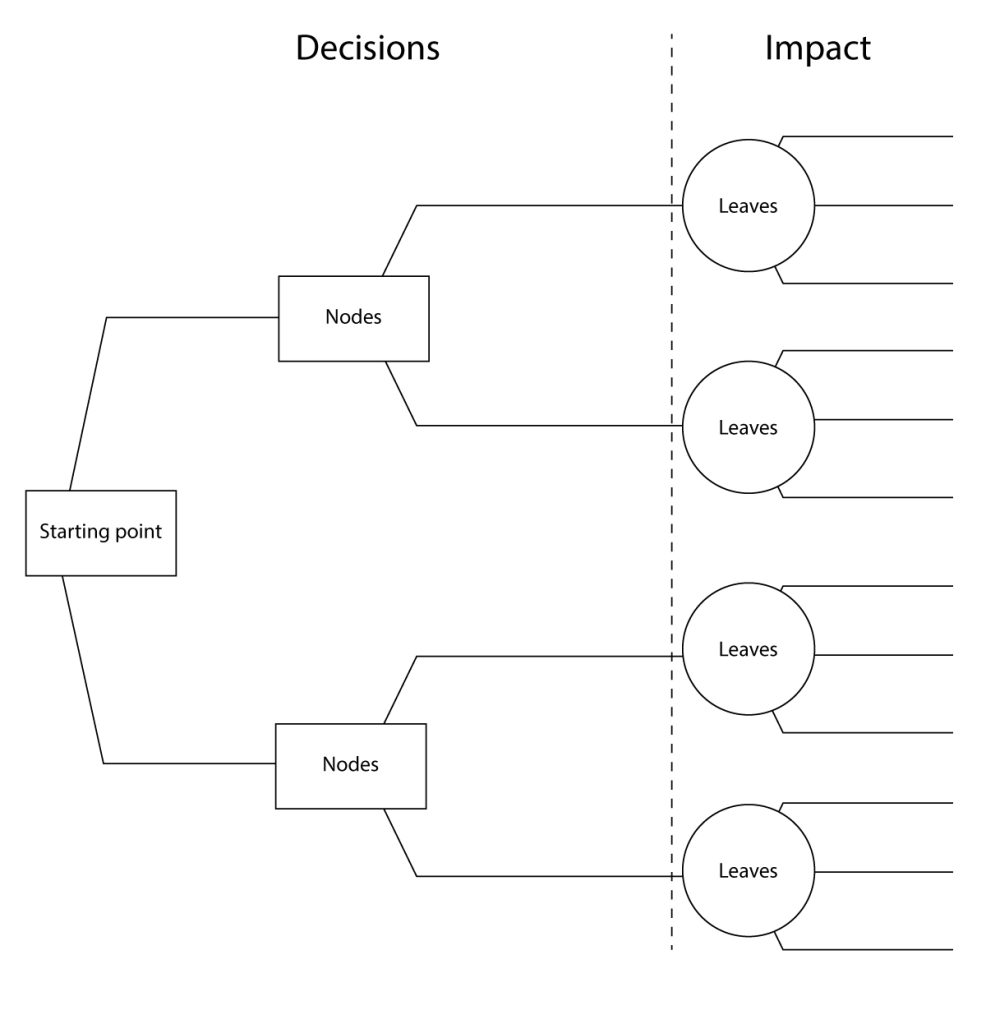
The decision trees are visual models that allow us to visually present all the different choices associated with a problem and describe each choice based on a probability value assigned to each choice outcome of a specific decision, which includes a group of related choices. The values of each choice are determined based on the probability value assigned to each expected outcome. In the decision trees, the prospective decisions are drawn in a hierarchy form that represents the relation between choices and outcomes. These outcomes are represented by two shapes: a square represents the decisions, while a circle represents the uncertain outcomes.
Related problem-solving articles:
- Problem-Solving Using Cause and Effect Diagram
- The Six Systems Thinking Steps to Solve Complex Problems
- Explore the 8D Problem Solving Approach
- Using the TRIZ Method for Creative Problem Solving
Drawing the Decision Trees
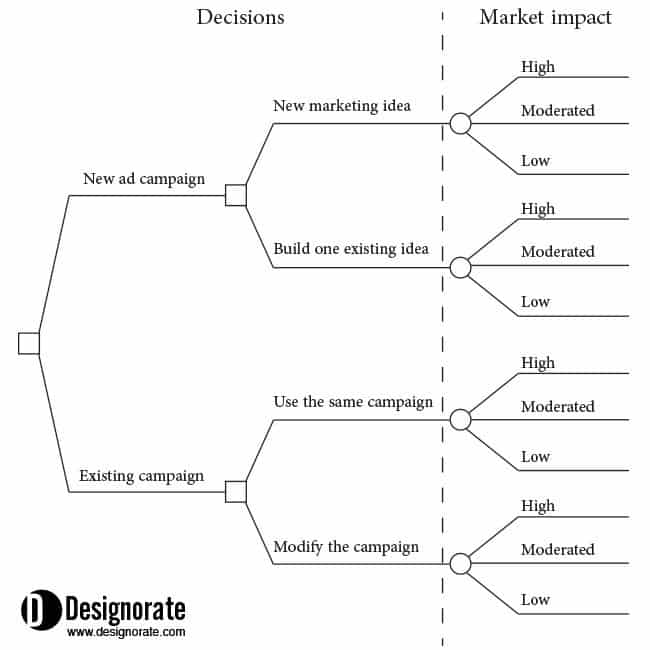
The decision tree starts with a small square that has branches, and each branch represents the available decision that needs to be considered during the decision-making process. Then, each of the branches can include more sub-branches based on the different choices that are available based on each decision branch. At the end of the branches, we tend to draw uncertainty lines that represent the expected outcomes from each branch.
In the below example, we assume that we need to make a decision of creating an advertising campaign for a television advertisement. So, we have two main choices: either to create a brand new campaign or to modify an existing campaign. In the new campaign branches, two other decisions may arise: use a new marketing idea or build the campaign based on the existing campaign idea. With the second choice, to use an existing campaign, we again have two decisions; here we can either use the campaign as it is or modify the existing campaign to increase its exposure.
Once the decisions are drawn and highlighted with the square shape as shown in the figure above, the uncertain outcomes are presented with a circle next to it. In this example, the outcomes indicate the market impact of the advertising campaign: low, moderated, or high.
Adding Rates and Values to the Decision Tree Outcome
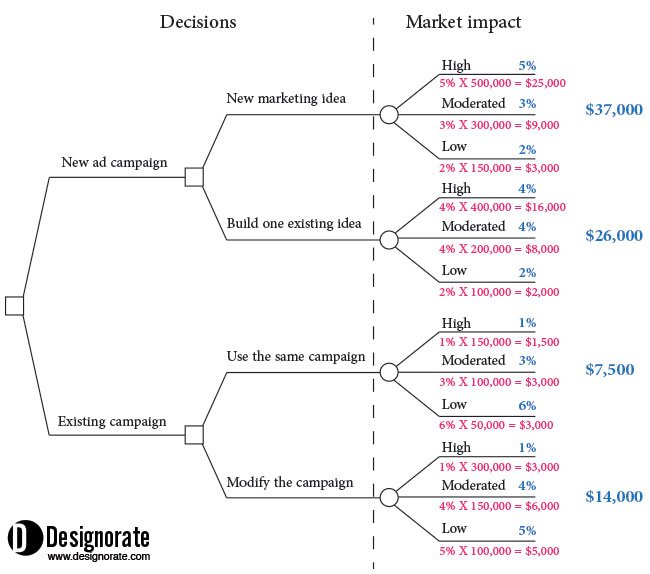
After completing the process of visualizing all the decisions and uncertain outcome on the decision tree, we need to add a rating for each outcome based on its expected strength. The rating can be either a percentage or a fraction of 1.0 for each outcome group. The total sum of all the values assigned to each decision outcome should not exceed a total of 100 percent or 1.0. For example, the below values can be assigned to the use a new marketing idea as follows: high (5%), moderated (3%), and low (2%). The percentage represent the probability of the outcome.
Then, we can write the expected gross revenues next to each of the expected outcomes. For example, if the market impact for creating a new advertising campaign is high, then the expected revenues for the company will reach $500,000. If the outcome is moderated, then the expected revenues will be $300,000.
After adding the probability value of each outcome and its expected revenues, the total outcome value is calculated by multiplying the probability value times the profit value. For example, the value for the new marketing idea option, would be as follows:
5% X 500,000 = $25,000
3% X 300,000 = $9,000
2% X 150,000 = $3,000
Calculating the Decision Value in the Decision Tree
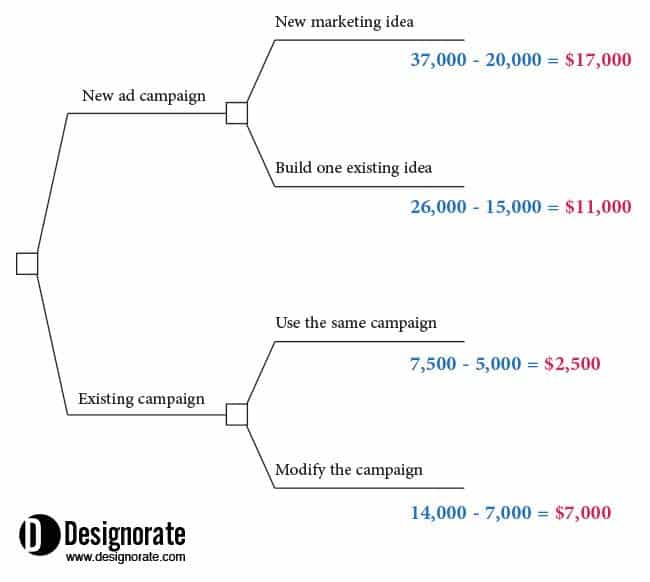
After indicating the expected value next to each outcome, the overall all value for each decision is calculated based on the sum of all the outcome possibilities minus the cost of each decision. For example, the total value of the three outcome possibilities in the first choice (a new marketing campaign) is:
25,000 (low) + 9,000 (moderated) + 3,000 (high) = $37,000
Then, we need to deduct the cost required to adopt this decision. In order to identify the next value of this specific decision, we would undertake the following:
37,000 (value) – 20,000 (cost)= $17,000 (net value)
So, the net value of the first decision (a new marketing campaign) will be $17,000. The same equation is applied to all the decisions in order identify a net value for each decision. Then, the final result will show the decision with the highest value which will be the proper decision to take.
When stuck for ideas, designers can depend on decision trees to give them a clue about the best decision to make based on calculating the probability of each decision and its values. While there are more complicated forms of the decision trees, the above example provides a simple and straightforward method to apply the decision trees as individuals or during meetings to identify the proper decisions. Furthermore, adding a visualization process to these decision-making processes allows for better understanding of the range of prospective options available.
